How to store numbers in Javascript
March 27, 2019
We know that all numbers in Javascript are stored in 64-bit format IEEE-754, also known as “double precision”,whatever the types int or float.
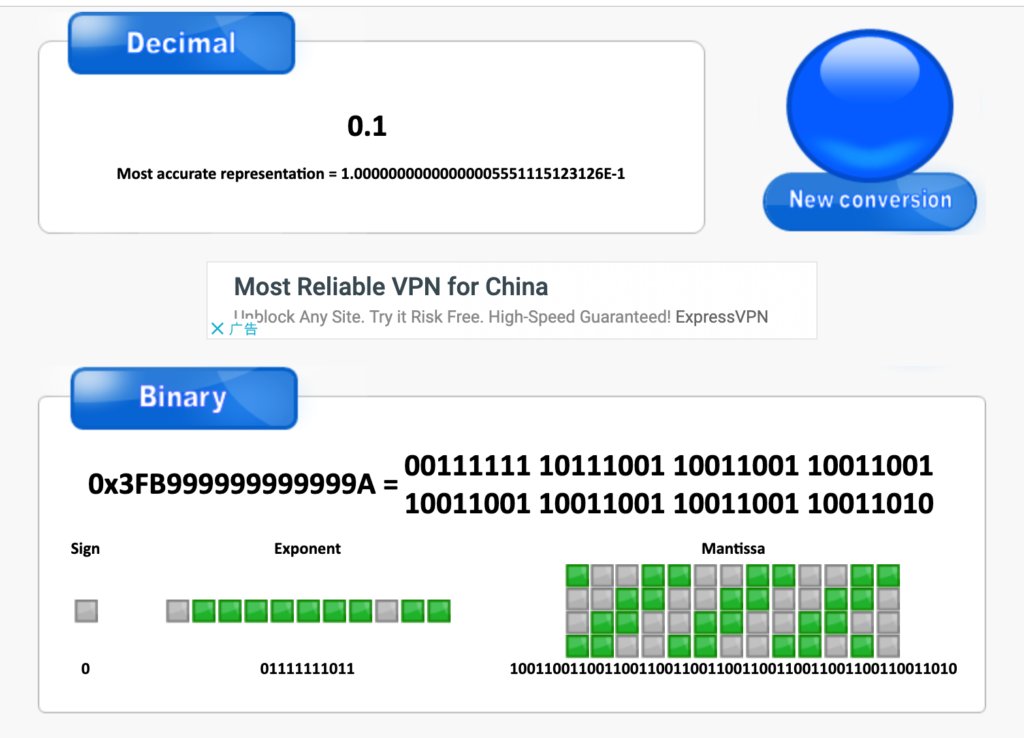
When you see a number for example 0.1, actually not 0.1, it is (0.1).toPrecision(30) => 0.100000000000000005551115123126. The number we see which precision is approximately 16 decimal digits,(0.100000000000000005551115123126).toPrecision(16) => 0.1000000000000000. So we see the 0.1 is 0.1。
1) 0.1(10) to binary number with 64-bit format
In IEEE-754, All number can be calculated using the following formula and 64-bit format:
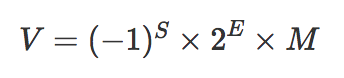
For example:
0.1 = (-1)0 * (0. 1001100110011001100110011001100110011001100110011010) * (2)1019
It contains sign(1 bit),exponent(11 bit) and mantissa(52 bit).
If the sign bit is 0, the number is positive, otherwise negative.
In 0.1,sign is 0,exponentis 1019 and mantissa is 1001100110011001100110011001100110011001100110011010.
Now we explain why they are in such numbers.- decimal transfer to binary
0.1 => 0.0001100110011001100110011001100110011…. - binary transfer to Scientific notation literal 0.0001100110011001100110011001100110011…. => 1.1 001100110011001100110011….* 2(-4)
- sign = 0, mantissa = 1.1 001100110011001100110011…. , exponent=-4.
- IEEE-754 1≤mantissa < 2,so the mantissa in all numbers is 1.XXXXXXXXX.so we remove 1, mantissa change to 1 001100110011001100110011…..
- we see that mantissa is 52 bits, so mantissa is 1001100110011001100110011001100110011001100110011010.
- The exponent is 11 bit long, meaning its lowest value is 0, its highest value is 2047 (211−1). To support negative exponents, the so-called offset binary encoding is used: 1023 is the zero, all lower numbers are negative, all higher numbers are positive. That means that you subtract 1023 from the exponent to convert it to a normal number. Therefore, the variable p that we previously used equals e−1023 and the significand is multiplied by 2e−1023 .so exponent=-4 to transter exponent = 1019.
- In a word, sign = 0, mantissa is 1001100110011001100110011001100110011001100110011010 and exponent = 1019, (1019)10 => (01111111011)2
- we see the 0.1, actually is stored in the following type.All kinds of operation is based on it.
2) (0)(01111111011)(1001100110011001100110011001100110011001100110011010)(2) with 64-bit format to decimal number
- (-1)0 * (0. 1001100110011001100110011001100110011001100110011010) * (2)1019 => (-1)0 * (0. 1001100110011001100110011001100110011001100110011010) * (2)-4
- (-1)0 * (0. 1001100110011001100110011001100110011001100110011010) * (2)-4 => (-1)0 * (1. 1001100110011001100110011001100110011001100110011010) * (2)-4
- (-1)0 * (1. 1001100110011001100110011001100110011001100110011010) * (2)-4 =>0.00011001100110011001100110011001100110011001100110011010(there are 56 bits after the point)
- 0.00011001100110011001100110011001100110011001100110011010 =>1/2-4 + 1/2-5 + 1/2-8 + 1/2-9 + 1/2-12 + 1/2-14 + ……+ 1/2-52 + 1/2-53 + 1/2-55 =>0.100000000000000005551115123126
- Now, 0.1=>0.100000000000000005551115123126
Now, This is just
0.1
=
00111111 10111001 10011001 10011001
10011001 10011001 10011001 10011010
=
0.100000000000000005551115123126